Pa315f8F4.png" alt="*">
Gợi Ý Bài Tập Ứng Dụng Đạo Hàm Trong Kinh Tế Và Cách Học Hiệu Quả
Xét mô hình kinh tế được biểu diễn qua hàm số $y=f(x)$ xác định và khả vi trên miền $D,$ trong đó coi $x$ là biến đầu vào và $y$ là biến đầu ra. Ta xét tại điểm $x={{x}_{0}}$ xem khi tăng $x$ thêm 1 đơn vị thì $y$ thay đổi như nào?
Ta có
\<\begin{gathered} f"({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}} \hfill \\ \Rightarrow \mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{f({x_0} + \Delta x) - f({x_0}) - f"({x_0})\Delta x}}{{\Delta x}} = 0 \hfill \\ \Rightarrow f({x_0} + \Delta x) - f({x_0}) - f"({x_0})\Delta x = o\left( {\Delta x} \right) \hfill \\ \Rightarrow f({x_0} + \Delta x) - f({x_0}) = f"({x_0})\Delta x + o\left( {\Delta x} \right) \hfill \\ \end{gathered} \>
Khi $\Delta x$ đủ nhỏ ta có $f({{x}_{0}}+\Delta x)-f({{x}_{0}})\approx {f}"({{x}_{0}})\Delta x.$
Cho $\Delta x=1\Rightarrow f({{x}_{0}}+1)-f({{x}_{0}})\approx {f}"({{x}_{0}}).$ Điều đó chưng tỏ tại $x={{x}_{0}}$ cho $x$ tăng 1 đơn vị thì $y$ tăng xấp xỉ ${f}"({{x}_{0}})$ đơn vị. Trong phân tích kinh tế, ${f}"({{x}_{0}})$ được gọi là giá trị cận biên của $y$ tại điểm ${{x}_{0}}.$
2. Hệ số co giãnXét mô hình kinh tế được biểu diễn qua hàm số $y=f(x)$ xác định và khả vi trên miền $D,$ trong đó coi $x$ là biến đầu vào và $y$ là biến đầu ra. Ta xét tại điểm $x={{x}_{0}}\in D$ xem khi tăng $x$ thêm 1% thì $y$ thay đổi như nào?
Giả sử tại điểm $x={{x}_{0}},$ thay đổi $x$ một lượng $\Delta x$ thì $y$ thay đổi một lượng $\Delta y({{x}_{0}})=f({{x}_{0}}+\Delta x)-f({{x}_{0}}).$
Phần trăm thay đổi của $x$ là $\dfrac{\Delta x}{{{x}_{0}}}100%;$ phần trăm thay đổi của $y$ là \<\dfrac{\Delta y({{x}_{0}})}{{{y}_{0}}}100%=\dfrac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{{{y}_{0}}}100%=\dfrac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x}.\dfrac{{{x}_{0}}}{{{y}_{0}}}\dfrac{\Delta x}{{{x}_{0}}}100%.\>
Vậy khi $x$ tăng thêm 1% thì $y$ thay đổi $\varepsilon _{x}^{y}%$ với \<\varepsilon _{x}^{y}=\dfrac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x}.\dfrac{{{x}_{0}}}{{{y}_{0}}}.\> Cho $\Delta x\to 0\Rightarrow \varepsilon _{x}^{y}={y}"({{x}_{0}}).\dfrac{{{x}_{0}}}{{{y}_{0}}}.$
Ý nghĩa kinh tế: Tại $x={{x}_{0}},$ khi $x$ tăng thêm 1% thì $y$ thay đổi một lượng khoảng $\varepsilon _{x}^{y}={y}"({{x}_{0}}).\dfrac{{{x}_{0}}}{{{y}_{0}}}$ %
+) Nếu $\varepsilon _{x}^{y}>0$ thì $y$ tăng $\varepsilon _{x}^{y}%.$
+) Nếu $\varepsilon _{x}^{y}3. Tối đa hoá lợi nhuận
CÁC VÍ DỤ MINH HOẠ
Câu 1: Giả sử hàm sản xuất của một doanh nghiệp $Q=5\sqrt{L}.$ Tính sản phẩm hiện vật cận biên của lao động tại mức sử dụng 100 đơn vị lao động và giải tích ý nghĩa của kết quả tìm được.
Bạn đang xem: Ứng dụng đạo hàm trong kinh tế
Ta có $MP{{P}_{L}}={Q}"(L)=\dfrac{5}{2\sqrt{L}}\Rightarrow MP{{P}_{L}}(100)=\dfrac{5}{2\sqrt{100}}=0,25.$ Điều này có ý nghĩa là tại mức sử dụng 100 đơn vị lao động, tăng thêm 1 đơn vị lao động thì sản lượng hiện vật tăng thêm khoảng 0,25 đơn vị hiện vật.
Câu 2:Một công ty độc quyền sản xuất một loại sản phẩm và tiêu thụ sản phẩm đó trên thị trường với hàm cầu $Q=1500-5p.$ Hãy tính doanh thu cận biên tại mức sản lượng $Q=650$ và giải tích ý nghĩa kết quả tìm được.
Ta có $Q=1500-5p\Leftrightarrow p=-\dfrac{1}{5}Q+300\Rightarrow TR(Q)=p
Q=-\dfrac{1}{5}{{Q}^{2}}+300Q.$
Do đó $MR=T{R}"(Q)=-\dfrac{2}{5}Q+300\Rightarrow MR(650)=40.$ Điều này có ý nghĩa tại mức sản lượng 650 nếu sản xuất thêm 1 đơn vị sản phẩm thì tổng doanh thu của công ty sẽ tăng thêm 40 đơn vị doanh thu.
Câu 3:Cho biết hàm doanh thu cận biên của doanh nghiệp sản xuất độc quyền 1 loại hàng hoá là $MR(Q)=40-0,45{{Q}^{2}}.$ Xác định hàm tổng doanh thu và hàm cầu hàng hoá của doanh nghiệp. Tính hệ số co giãn của cầu theo giá tại mức giá $p=30$ và nêu ý nghĩa của kết quả tính được.
Ta có $TR=\int{MR(Q)d
Q}=\int{\left( 40-0,45{{Q}^{2}} \right)d
Q}=40Q-0,15{{Q}^{3}}+{{C}_{0}}.$
Vì $TR(0)=0\Leftrightarrow {{C}_{0}}=0\Rightarrow TR=40Q-0,15{{Q}^{3}}=p
Q\Rightarrow p=40-0,15{{Q}^{2}}\Leftrightarrow Q=\sqrt{\dfrac{40-p}{0,15}}\left( Q>0 \right).$
Ta có $\varepsilon _{p}^{Q}={Q}"(p).\dfrac{p}{Q}=\dfrac{-1}{2\times 0,15\sqrt{\dfrac{40-p}{0,15}}}.\dfrac{p}{Q}=-\dfrac{p}{2(40-p)}\Rightarrow \varepsilon _{p}^{Q}(p=30)=-1,5.$
Tại mức giá $p=30$ nếu tăng giá 1% thì lượng cầu giảm khoảng 1,5%.
Câu 4:Một nhà sản xuất độc quyền bán sản phẩm trên thị trường có hàm cầu ngược $p=1400-7,5Q.$ Hãy xác định hệ số co giãn của cầu theo giá tại mỗi mức giá $p.$ Xác định mức sản lượng cho lợi nhuận tối đa, cho biết hàm chi phí cận biên $MC=3{{Q}^{2}}-12Q+140.$
Có $p=1400-7,5Q\Leftrightarrow Q=\dfrac{560}{3}-\dfrac{2}{15}p\Rightarrow \varepsilon _{p}^{Q}={Q}"(p).\dfrac{p}{Q}=-\dfrac{2}{15}.\dfrac{p}{\dfrac{560}{3}-\dfrac{2}{15}p}.$
Hàm lợi nhuận của doanh nghiệp là
$\pi =TR-TC=\left( 1400Q-7,5{{Q}^{2}} \right)-\left( {{Q}^{3}}-6{{Q}^{2}}+140Q \right)=-{{Q}^{3}}-1,5{{Q}^{2}}+1260Q.$
+) Điều kiện cần: ${\pi }"=0\Leftrightarrow -3{{Q}^{2}}-3Q+1260=0\Leftrightarrow Q=20\left( Q>0 \right).$
+) Điều kiện đủ: ${\pi }""=-6Q-3\Rightarrow {\pi }""(20)=-123
Khoá học cung cấp đầy đủ kiến thức và phương pháp giải bài tập các dạng toán đi kèm mỗi bài học. Hệ thống bài tập rèn luyện dạng Tự luận có lời giải chi tiết tại website sẽ giúp học viên học nhanh và vận dụng chắc chắn kiến thức. Mục tiêu của khoá học giúp học viên đạt điểm A thi cuối kì các học phần Toán cao cấp 1 và Toán cao cấp 2 trong các trường kinh tế.
Sinh viên các trường ĐH sau đây có thể học được combo này:
- ĐH Kinh Tế Quốc Dân
- ĐH Ngoại Thương
- ĐH Thương Mại
- Học viện Tài Chính
- Học viện ngân hàng
- ĐH Kinh tế ĐH Quốc Gia Hà Nội
và các trường đại học, ngành kinh tế của các trường ĐH khác trên khắp cả nước...


tương đương chương trình Giải tích 1 và Giải tích 2 khối ngành kỹ thuật.
Các bài tập ứng dụng đạo hàm trong kinh tế thường sẽ có nhiều kiến thức khó để học sinh luyện tập. Nhưng nếu chinh phục được dạng toán này sẽ rất có ích cho tương lai của mọi người vì tính ứng dụng của chúng cực kỳ cao.
Ứng dụng đạo hàm trong kinh tế là gì?
Vốn dĩ toán học đã có tính ứng dụng trong kinh tế rất cao từ việc đi chợ, mua bán, tính toán chi phí… Đặc biệt, với chương đạo hàm này thì được ứng dụng trong kinh tế là chủ yếu để biết được tốc độ tăng trưởng kinh tế nhằm đưa ra những quyết định đầu tư đúng đắn.
Rất đơn giản! đầu tiên mọi người sẽ sử dụng hàm số mô tả đại lượng về kinh tế đang quan tâm, rồi tiếp đến chỉ cần áp dụng công thức tính đạo hàm để đạo hàm nó để có thể dự đoán được tốc độ tăng trưởng của doanh nghiệp trong tương lai.
Ngoài ra, trong lĩnh vực kinh tế, đạo hàm còn ứng dụng tuyệt vời trong việc dự đoán xem hàm số cần tính toán đạt giá trị nhỏ nhất hay lớn nhất ở đâu, để từ đó giúp doanh nghiệp tối ưu hóa các hoạt động khác nhau một cách hiệu quả.

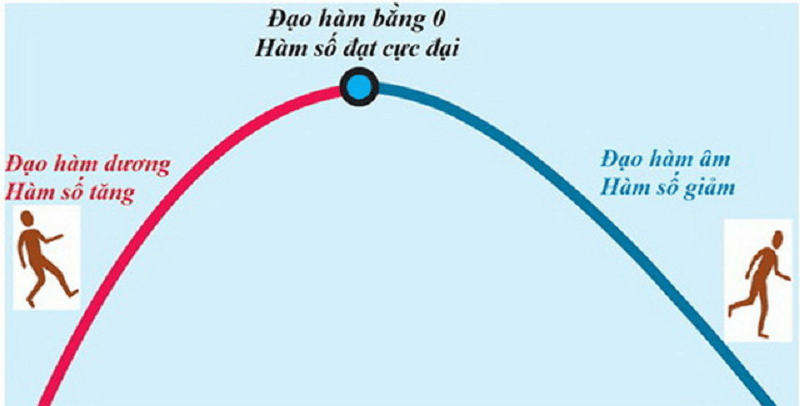
Cụ thể nếu đạo hàm dương (hàm số đang tăng) rồi bỗng dưng chuyển sang đạo hàm âm (hàm số giảm). Lúc này nó đã đi qua vị trí mà hàm số đạt giá trị cực đại, cũng là nơi có đạo hàm bằng 0.
Từ nhận xét này, bằng việc tìm những vị trí có đạo hàm bằng 0, người ta sẽ biết được có một đại lượng sẽ đạt giá trị nhỏ nhất và lớn nhất ở đâu, để tối ưu hóa nó theo mong muốn.
Đặc biệt, dựa vào điểm này, công ty sẽ dễ dàng tính được số sản phẩm nên sản xuất bao nhiêu để đạt được lợi nhuận tốt nhất.
Công thức tính đạo hàm trong kinh tế
Công thức tính bài tập đạo hàm lợi nhuận của nhà sản xuất như sau:
p=- 1/3Q3 + 14Q2 + 60Q - 54
Trong đó:
p là lợi nhuận của nhà sản xuấtQ là mức sản lượng cho lợi nhuận p
Bài tập ứng dụng đạo hàm trong kinh tế như thế nào?
Trong kinh tế, toán học mang một ý nghĩa cực kỳ to lớn giúp doanh nghiệp có thể tính toán được kết quả và mục tiêu mình đặt ra. Đặc biệt, với chuyên đề toán đạo hàm chúng thường được ứng dụng trong kinh tế với những dạng bài tập cơ bản như:
Đạo hàm và xu hướng biến thiên của hàm số
Ở dạng toán đạo hàm trong kinh tế này sẽ phải giải quyết 2 vấn đề là sự liên hệ giữa đạo hàm và xu hướng biến thiên của hàm số, cùng với việc xác định được khoảng tăng giảm của hàm số. cụ thể:
Định lý 1: Điều kiện cần
Nếu hàm số f(x) có đạo hàm tại mọi điểm thuộc khoảng (a;b) thì:
f(x) đơn điệu tăng trên khoảng (a;b) => f’(x) ³ 0, "xÎ (a;b)f(x) đơn điệu giảm trên khoảng (a;b) => f’(x) £ 0, "xÎ (a;b)Định lý 2: Điều kiện đủ
Nếu hàm số f(x) có đạo hàm tại mọi điểm thuộc khoảng (a;b) thì:
f’(x) > 0, "xÎ(a;b) => f(x) đơn điệu tăng trên khoảng (a;b)f’(x) "xÎ(a;b) => f(x) đơn điệu giảm trên khoảng (a;b)f’(x) = 0,"xÎ(a;b)=> f(x) có giá trị không đổi trên khoảng (a;b)Xác định khoảng tăng giảm của một hàm số
Để có thể tính toán được khoảng tăng và giảm của mộ hàm số y = f(x) trong kinh tế, mọi người dựa vào những bước sau:
Bước 1: Xác định được miền xác định của một hàm sốBước 2: Tính đạo hàm y’ tương ứng của hàm sốBước 3: Tiến hành xét dấu của đạo hàm vừa tính được.Bước 4: Từ bảng xét dấu đạo hàm, tiến hành đưa ra kết luận khoảng tăng hay giảm của hàm số tương ứng.Ví dụ:

Tìm các điểm cực trị của hàm số
Định nghĩa: Cho hàm số f(x) xác định liên tục trên khoảng (a;b). Trong đó:
f(x) được gọi là đạt cực đại tại điểm x0 Î(a;b) nếu $d > 0 sao cho: "xÎ(a;b), 0 0| d Þ f(x) 0)f(x) được gọi là đạt cực tiểu tại điểm x0 Î(a;b) nếu $d > 0 sao cho: "xÎ(a;b), 0 0| d Þ f(x) > f(x0)Trong đó, điểm cực tiểu và cực đại sẽ được gọi chung là điểm cực trị của một hàm số.

Vậy nên, để có thể tìm được điểm cực trị của hàm số trong bài tập ứng dụng đạo hàm trong kinh tế, đòi hỏi phải nắm được điều kiện cần và điều kiện đủ của chúng. Cụ thể:
Điều kiện cần:
Nếu hàm số f(x) đạt cực trị tại x0Î(a;b) và f(x) có đạo hàm tại x0 thì: f ’(x0) = 0
Kết luận: Hàm số f(x) đưa ra chỉ có thể đạt được giá trị cực đại tại một điểm giới hạn tương ứng là – , chúng thuộc một trong hai loại là điểm dừng (điểm mà đạo hàm tại khoảng đó bị triệt tiêu) và điểm mà tại khoảng đó hàm số liên tục nhưng không có đạo hàm.
Điều kiện đủ:
Giả sử x0 là một trong những điểm tới hạn của một hàm số và đạo hàm của chúng có dấu xác định trên khoảng (x0 – d; x0), (x0; x0+ d) của x0.
Nếu chúng đi qua điểm x0 với đạo hàm tương ứng đổi dấu thì hàm số đó sẽ đạt cực trị tại chính điểm đó
X0 là điểm cực đại nếu f ’(x) đổi dấu từ + sang –;X0 là điểm cực tiểu nếu f ’(x) đổi dấu từ – sang +;Nếu qua điểm X0mà đạo hàm không đổi dấu thì hàm số sẽ không đạt cực trị tại điểm đó.Các bước tìm cực trị của một hàm số
Để có thể tìm được cực trị của hàm số y = f(x) cho trước thì các em có thể áp dụng các bước sau:
Bước 1: Tính miền xác định của hàm số tương ứngBước 2: Tính đạo hàm của hàm sốBước 3: Tính điều kiện cần của hàm số để tìm điểm tới hạn. Bao gồm tìm các điểm dừng hoặc chỉ ra những điểm thuộc miền xác định tại đó hàm liên tục nhưng không có đạo hàm.Bước 4: Xét điều kiện đủ của đạo hàm với từng điểm tới hạn và kết luận tương ứng.Ví dụ:

Ý nghĩa của bài tập ứng dụng đạo hàm trong kinh tế
Về việc xác định ý nghĩa của đạo hàm trong kinh tế sẽ tiến hành tính toán đạo hàm và giá trị cận biên trong kinh tế, cũng như đạo hàm cấp hai kèm theo quy luật lợi ích cận biên giảm dần. Cụ thể
Đạo hàm và giá trị cận biên trong kinh tếỞ đây sẽ tiến hành tính đạo hàm cấp 1 và giá trị cận biên. Cụ thể, khi xét trên mô hình hàm số y = f(X), trong đó x và y chính là những biến số kinh tế.
Lúc này, giá trị y – cận biên của x tại x = x0 (Mf(x0)) chính là giá trị mô tả sự thay đổi giá trị của chính y khi x biến đổi 1 đơn vị tại giá trị ban đầu x = x0, tương ứng là Mf(x0) = f(x0+1) – f(x0).
Khi liên hệ với đạo hàm ta có: Mf(x0) = f(x0+1) – f(x0) ≈ f ’(x0).
Một số mô hình hàm cận biên như:
Hàm chi phí sản xuất: TC = TC(Q)Chi phí cận biên: MC = TC’(Q)Hàm doanh thu: TR = TR(Q)Doanh thu cận biên: MR = TR’(Q)Hàm lợi ích: U = U(x)Lợi ích cận biên: MU = U’(x)Hàm sản xuất ngắn hạn: Q = f(L)Giá trị sản phẩm hiện vật cận biên của lao động: MPPL = f’(L).
Dựa trên mô hình hàm số y = f(x), trong đó y chính là biến số biểu diễn lợi ích của doanh nghiệp (ví dụ như lợi nhuận, doanh thu, thu nhập…) còn x chính là biến số mô tả yếu tố mang lại giá trị y.
Quy luật lợi ích cận biên sẽ giảm dần nói rằng x càng lớn thì y cận biên càng nhỏ. Đồng thời điều kiện đểMy giảmÛ f”(x)£0.
Tính hệ số co giãn của cung và cầu theo giá
Việc tính hệ số co dãn của cầu theo giá chính là việc tính số do lượng thay đổi tính dựa trên % của lượng cầu khi giá tăng 1%.
Ở đây, ta có hàm cầu QD = D(p), tương ứng. e
D = D’(p). p/D(p)
Còn hệ số co giãn của cung theo giá chính là việc tính toán số đo lường thay đổi tính dựa trên % của lượng cung khi giá tăng 1%.
Ở đây, ta có hàm cung QS = S(p), tương ứng. e
S = S’(p). p/S(p)

Sự lựa chọn tối ưu trong kinh tế
Lựa lựa chọn tối ưu trong kinh tế dựa vào đạo hàm sẽ tiến hành chọn mức sản lượng tối ưu cùng với việc chọn tối ưu mức sử dụng dựa trên yếu tố đầu vào. Cụ thể:
Chọn mức sản lượng tối ưuTổng chi phí: TC = TC(Q)Tổng doanh thu: TR = TR(Q).Yêu cầu cần phải chọn mức sản lượng Q sao cho lợi nhuận tối đa?
Cách giải:
Tìm Q sao cho p = TR(Q) – TC(Q) đạt giá trị cực đại. Điều kiện cần chính là p’ = TR’(Q) – TC’(Q) = 0 Û MR = MC.
Lúc này, lợi nhuận sẽ đạt tối đa nếu doanh thu cận biên của công ty sẽ phải bằng chi phí cần biên. Tương ứng với điều kiện đủ chính là: p”ÛTR”(Q) > Û TR’’(Q) Lựa chọn tối ưu mức sử dụng dựa vào yếu tố đầu vào Ở đây mọi người sẽ sử dụng: Lúc này hãy lựa chọn mức sử dụng lao động sao cho tiết kiệm chi phí, đạt lợi nhuận tối đa? Cách giải:Đầu tiên cần phải tìm L sao cho p = p.f(L) – w Điều kiện cần tương ứng là p’=0 Û p.MPPL – w Điều kiện đủ là khi p”Ûf ”(L) >Û f ‘’(L) Công thức đạo hàm nâng cao 11 và tuyệt chiêu giải bài tập cực đỉnh học sinh nên biết Trên đây là tổng hợp những thông tin cung cấp về ý nghĩa và tầm quan trọng của bài tập ứng dụng đạo hàm trong kinh tế. Qua đó có thể thấy toán học là môn quan trọng, mang đến nhiều giá trị hỗ trợ việc kinh tế một cách tốt hơn.
L; chi phí cố định là C0
L.L – C0 đạt được giá trị cực đại.
L = 0. Lúc này, lợi nhuận sẽ đạt tối đa nếu giá trị bằng tiền của sản phẩm hiện vật cận biên của lao động sẽ bằng với giá thuê lao động.
Xem thêm: Hướng dẫn căn lề trong word 2007, 2010, 2013, 2016, 2019, cách căn lề trong word cực chuẩn chỉKết luận