
Câu hỏi: Tung Độ Là X Hay Y?
=> Tung độ là trục Oy.
Bạn đang xem: Hoành độ là x hay y
Kiến thức liên quan – Tung Độ Là X Hay Y
Trục tung, trục hoành là gì?Hệ tọa độ Oxy gồm 2 trục, trục tung là trục dọc thẳng đứng, trục hoành là trục nằm ngang.
Chúng ta có thể hiểu đơn giảný nghĩa của hai từ tung và hoành: Tung là dọc, hoành là ngang. Và vì lẽ đó mà người ta mới gọi trục dọc là trục tung, trục ngang là trục hoành.
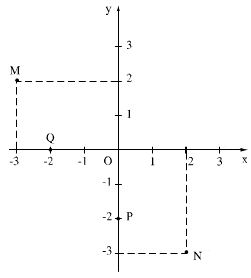
Toạ độ của một điểm trong mặt phẳng toạ độ:
Trên mặt phẳng toạ độ, mỗi điểm M xác định một cặp số (x0; y0). Ngược lại mỗi cặp số (x0; y0) xác định vị trí của một điểm M. Kí hiệu M(x; y)Cặp số (x0; y0) gọi là toạ độ của điểm M; x0là hoành độ và y0là tung độ của điểm M.Chú ý:
Bao giờ cũng viết hoành độ trước, tung độ sau.Toạ độ điểm gốc O là (0; 0); O(0;0).Để tìm toạ độ của một điểm M, từ M ta kẻ các đường vuông góc MH⊥Ox, MK⊥Oyvà đọc kết quả:Toạ độ của điểm H trên Ox là hoành độ điểm MToạ độ của điểm K trên Oy là tung độ của điểm M.Bài tập vận dụng
Câu 1. Trên hệ trục toạ độ Oxy lấy điểm A. Điểm A(x; y) nằm ở góc phần tư nào, nếu:
x > 0, y > 0. b. x > 0, y x 0. d. x Hướng dẫn giải:Nếu x > 0, y > 0 thì A(x; y) ở góc phần tư I.Nếu x > 0, y Nếu x 0 thì A(x; y) ở góc phần tư II.Nếu x
Câu 2. Tìm trên mặt phẳng toạ độ Oxy tất cả các điểm có:
Hoành độ bằng 0. b. Tung độ bằng 0.Hoành độ bằng 1. d. Tung độ bằng -2.Hoành độ bằng số đối của tung độ.Hoành độ bằng tung độ.Hướng dẫn giải:Tất cả các điểm nằm trên trục tung Oy.Tất cả các điểm trên trục hoành Ox.Tất cả các điểm nằm trên đường thẳng song song với trục tung và cắt trục hoành tại điểm 1.Tất cả các điểm nằm trên đường thẳng song song với trục hoành và cắt trục tung tại điểm -2.Tất cả các điểm nằm trên đường thẳng chứa các tia phân giác của góc phần tư II và IV.Tất cả các điểm nằm trên đường thẳng chứa các tia phân giác của góc phần tư I và III.
Ghi nhớ:
Trục tung Oy là tập hợp các điểm có hoành độ bằng 0: M(0;b)Trục hoành Ox là tập hợp các điểm có tung độ bẳng 0: M(a;0)Bài viết trên đây giải đáp về thắc mắc Tung Độ Là X Hay Y. Cùng với đó là những kiến thức liên quan mà Hocvn tổng hợp được. Mong rằng bài viết trên hữu ích với bạn.
a) Trục toạ độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O gọi là điểm gốc và một vectơ đơn vị $\overrightarrow e $.
Ta kí hiệu trục đó là (O ; $\overrightarrow e $)

b) Cho M là một điểm tuỳ ý trên trục (O ; $\overrightarrow e $). Khi đó có duy nhất một số k sao cho $\overrightarrow {OM} = k\overrightarrow e $. Ta gọi số k đó là toạ độ của điểm M đối với trục đã cho.
c) Cho hai điểm A và B trên trục (O ; $\overrightarrow e $). Khi đó có duy nhất số a sao cho $\overrightarrow {AB} = a\overrightarrow e $. Ta gọi số a đó là độ dài đại số của vectơ $\overrightarrow {AB} $ đối với trục đã cho và kí hiệu $a = \overline {AB} $.
Nhận xét
Nếu$\overrightarrow {AB} $ cùng hướng với $\overrightarrow e $ thì $\overline {AB} = AB$, còn nếu$\overrightarrow {AB} $ ngược hướng với $\overrightarrow e $ thì $\overline {AB} = - AB$.
Nếu hai điểm A và B trên trục (O ; $\overrightarrow e $) có toạ đô lần lượt là a và b thì $\overline {AB} = b - a$.
2. Hệ trục tọa độ
a) Định nghĩa
Hệ trục toạ độ $\left( {O;\overrightarrow i ;\overrightarrow j } \right)$ gồm hai trục $\left( {O;\overrightarrow i } \right)$ và $\left( {O;\overrightarrow j } \right)$ vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc toạ độ. Trục$\left( {O;\overrightarrow i } \right)$được gọi là trục hoành và kí hiệu là Ox, trục $\left( {O;\overrightarrow j } \right)$ được gọi là trục tung và kí hiệu là Oy. Các vectơ $\overrightarrow i $ và $\overrightarrow j $ là các vectơ đơn vị trên Ox và Oy và $\left| {\overrightarrow i } \right| = \left| {\overrightarrow j } \right| = 1$. Hệ trục toạ độ$\left( {O;\overrightarrow i ;\overrightarrow j } \right)$còn được kí hiệu là Oxy.

b) Tọa độ của vectơ
$\overrightarrow u = \left( {x;y} \right) \Leftrightarrow \overrightarrow u = x\overrightarrow i + y\overrightarrow j $
Nhận xét
Từ định nghĩa toạ độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Xem thêm: Transformers: siêu người máy biến hình phần 2, robot đại chiến
Nếu $\overrightarrow u = \left( {x;y} \right);\overrightarrow {u"} = \left( {x";y"} \right)$ thì
$\overrightarrow u = \overrightarrow {u"} \Leftrightarrow \left\{ \begin{array}{l} x = x"\\ y = y" \end{array} \right.$
Như vậy, mỗi vectơ được hoàn toàn xác định khi biết toạ độ của nó.
c) Toạ độ của một điểm
Trong mặt phẳng toạ độ Oxy cho một điểm M tuỳ ý. Toạ độ của vectơ $\overrightarrow {OM} $ đối với hệ trục Oxy được gọi là toạ độ của điểm M đối với hệ trục đó.

$M = \left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j $
Chú ý: nếu $M{M_1} \bot Ox,M{M_2} \bot Oy$ thì $x = \overline {O{M_1}} ,y = \overline {O{M_2}} $.
d) Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho điểm $A\left( {{x_A};{y_A}} \right)$ và $B\left( {{x_B};{y_B}} \right)$. Ta có:
$\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$
3. Tọa độ của các vectơ $\overrightarrow u + \overrightarrow v ,\overrightarrow u - \overrightarrow v ,k\overrightarrow u $
Ta có các công thức sau:
Cho $\overrightarrow u = \left( {{u_1};{u_2}} \right),\overrightarrow v = \left( {{v_1};{v_2}} \right)$. Khi đó:
$\begin{gathered} \overrightarrow u + \overrightarrow v = \left( {{u_1} + {v_1};{u_2} + {v_2}} \right); \hfill \\ \overrightarrow u - \overrightarrow v = \left( {{u_1} - {v_1};{u_2} - {v_2}} \right); \hfill \\ k\overrightarrow u = \left( {k{u_1};k{u_2}} \right),k \in R \hfill \\ \end{gathered} $
4. Tọa độ trung điểm của đoạn thẳng. Tọa độ của trọng tâm tam giác
a) Cho đoạn thẳng AB có $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$. Ta dễ dàng chứng minh được toạ độ trung điểm $I\left( {{x_I};{y_I}} \right)$ của đoạn thẳng AB là :
${x_I} = \frac{{{x_A} + {x_B}}}{2};{y_I} = \frac{{{y_A} + {y_B}}}{2}$
b) Cho tam giác ABC có $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)$. Khi đó toạ đô của trọng tâm $G\left( {{x_G};{y_G}} \right)$ của tam giác ABC được tính theo công thức:
${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}$